Decision trees serve various purposes in machine learning, including classification, regression, feature selection, anomaly detection, and reinforcement learning. They operate using straightforward if-else statements until the tree’s depth is reached. Grasping certain key concepts is crucial to fully comprehend the inner workings of a decision tree.
Two critical concepts to grasp when exploring decision trees are entropy and information gain. Entropy quantifies the impurity within a set of training examples. A training set containing only one class exhibits an entropy of 0, while a set with an equal distribution of examples from all classes has an entropy of 1. Information gain, conversely, represents the decrease in entropy or impurity achieved by dividing the training examples into subsets based on a specific attribute. A strong comprehension of these concepts is valuable for understanding the inner mechanics of decision trees.
We will develop a decision tree class and define essential attributes required for making predictions. As mentioned earlier, entropy and information gain are calculated for each feature before deciding on which attribute to split. In the training phase, nodes are divided, and these values are considered during the inference phase for making predictions. We will examine how this is accomplished by going through the code segments.
The initial step involves creating a decision tree class, incorporating methods and attributes in subsequent code segments. This article primarily emphasizes constructing decision tree classifiers from the ground up to facilitate a clear comprehension of complex models’ inner mechanisms. Here are some considerations to keep in mind when developing a decision tree classifier.

In this code segment, we define a decision tree class with a constructor that accepts values for max_depth, min_samples_split, and min_samples_leaf. The max_depth attribute denotes the maximum depth at which the algorithm can cease node splitting. The min_samples_split attribute considers the minimum number of samples required for node splitting. The min_samples_leaf attribute specifies the total number of samples in the leaf nodes, beyond which the algorithm is restricted from further division. These hyperparameters, along with others not mentioned, will be utilized later in the code when we define additional methods for various functionalities.
This concept pertains to the uncertainty or impurity present in the data. It is employed to identify the optimal split for each node by calculating the overall information gain achieved through the split.

This code computes the overall entropy based on the count of samples for each category in the output samples. It is important to note that the output variable may have more than two categories (multi-class), making this model applicable for multi-class classification as well. Next, we will incorporate a method for calculating information gain, which aids the model in splitting examples based on this value. The following code snippet outlines the sequence of steps executed.

A threshold is defined below, which divides the data into left and right nodes. This process is carried out for all feature indexes to identify the best fit. Subsequently, the resulting entropy from the split is recorded, and the difference is returned as the total information gain resulting from the split for a specific feature. The final step involves creating a split_node function that executes the splitting operation for all features based on the information gain derived from the split.
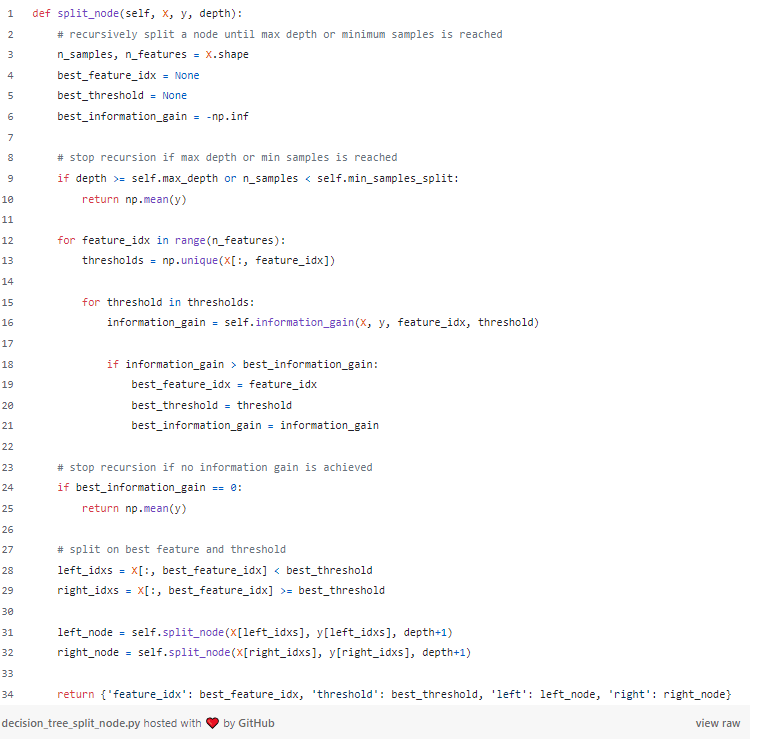
We initiated the process by defining key hyperparameters such as max_depthand min_samples_leaf. These factors play a crucial role in the split_node method as they determine if further splitting
should occur. For instance, when the tree reaches its maximum depth or when the minimum number of samples is met, data splitting ceases.
Once the minimum samples and maximum tree depth conditions are satisfied, the next step involves identifying the feature that offers the highest information gain from the split. To achieve this, we iterate through all features, calculating the total entropy and information gain resulting from the split based on each feature. Ultimately, the feature yielding the maximum information gain serves as a reference for dividing the data into left and right nodes. This process continues until the tree’s depth is reached and the minimum number of samples are accounted for during the split.

Moving forward, we employ the previously defined methods to fit our model. The split_node function is instrumental in computing the entropy and information gain derived from partitioning the data into
two subsets based on different features. As a result, the tree attains its maximum depth, allowing the model to acquire a feature representation that streamlines the inference process.
The split_node function accepts a set of attributes, including input data, output, and depth, which is a hyperparameter. The function traverses the decision tree based on its initial training with the
training data, identifying the optimal set of conditions for splitting. As the tree is traversed, factors such as depth, minimum number of samples, and minimum number of leaves play a role in determining the final prediction.
Once the decision tree is constructed with the appropriate hyperparameters, it can be employed to make predictions for unseen or test data points. In the following sections, we will explore how the model handles predictions for new
data, utilizing the well-structured decision tree generated by the split_node function.

We are going to define the predict function that accepts the input and makes predictions for every instance. Based on the threshold value that was defined earlier to make the split, the model would traverse through the tree until the outcome is obtained for the test set. Finally, predictions are returned in the form of arrays to the users.
This predict method serves as a decision-making function for a decision tree classifier. It starts by initializing an empty list, y_pred, to store the predicted class labels for a given set
of input values. The algorithm then iterates over each input example, setting the current node to the decision tree's root.
As the algorithm navigates the tree, it encounters dictionary-based nodes containing crucial information about each feature. This information helps the algorithm decide whether to traverse towards the left or right child node, depending on the feature value and the specified threshold. The traversal process continues until a leaf node is reached.
Upon reaching a leaf node, the predicted class label is appended to the y_pred list. This procedure is repeated for every input example, generating a list of predictions. Finally, the list of predictions is converted into
a NumPy array, providing the predicted class labels for each test data point in the input.
In this subsection, we will examine the output of a decision tree regressor model applied to a dataset for estimating AirBnb housing prices. It is important to note that analogous plots can be generated for various cases, with the tree’s depth and other hyperparameters indicating the complexity of the decision tree.
In this section, we emphasize the interpretability of machine learning (ML) models. With the burgeoning demand for ML across various industries, it is essential to not overlook the importance of model interpretability. Rather than treating these models as black boxes, it is vital to develop tools and techniques that unravel their inner workings and elucidate the rationale behind their predictions. By doing so, we foster trust in ML algorithms and ensure responsible integration into a wide range of applications.
Note: The dataset was taken from New York City Airbnb Open Data | Kaggle under Creative Commons — CC0 1.0 Universal License
Decision tree regressors and classifiers are renowned for their interpretability, offering valuable insights into the rationale behind their predictions. This clarity fosters trust and confidence in model predictions by aligning them with domain knowledge and enhancing our understanding. Moreover, it enables opportunities for debugging and addressing ethical and legal considerations.
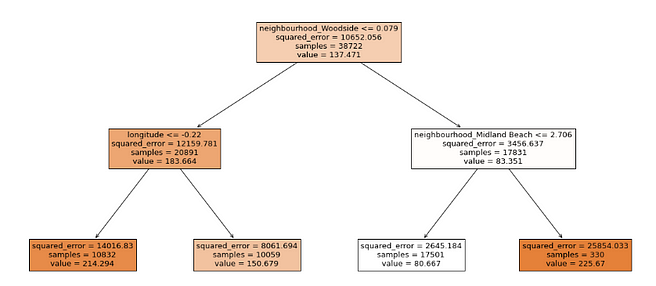
After conducting hyperparameter tuning and optimization, the optimal tree depth for the AirBnb home price prediction problem was determined to be 2. Utilizing this depth and visualizing the results, features such as the Woodside neighborhood, longitude, and Midland Beach neighborhood emerged as the most significant factors in predicting AirBnb housing prices.
Upon completing this article, you should possess a robust understanding of decision tree model mechanics. Gaining insights into the model’s implementation from the ground up can prove invaluable, particularly when employing scikit-learn models and their hyperparameters. Additionally, you can customize the model by adjusting the threshold or other hyperparameters to enhance performance. Thank you for investing your time in reading this article.
Below are the ways where you could contact me or take a look at my work.
GitHub: suhasmaddali (Suhas Maddali ) (github.com)
YouTube: https://www.youtube.com/channel/UCymdyoyJBC_i7QVfbrIs-4Q
LinkedIn: (1) Suhas Maddali, Northeastern University, Data Science | LinkedIn
Medium: Suhas Maddali — Medium